Thresholding
Last updated on 2025-02-09 | Edit this page
Estimated time: 110 minutes
Overview
Questions
- How can we use thresholding to produce a binary image?
Objectives
- Explain what thresholding is and how it can be used.
- Use histograms to determine appropriate threshold values to use for the thresholding process.
- Apply simple, fixed-level binary thresholding to an image.
- Explain the difference between using the operator
>or the operator<to threshold an image represented by a NumPy array. - Describe the shape of a binary image produced by thresholding via
>or<. - Explain when Otsu’s method for automatic thresholding is appropriate.
- Apply automatic thresholding to an image using Otsu’s method.
- Use the
np.count_nonzero()function to count the number of non-zero pixels in an image.
In this episode, we will learn how to use scikit-image functions to apply thresholding to an image. Thresholding is a type of image segmentation, where we change the pixels of an image to make the image easier to analyze. In thresholding, we convert an image from colour or grayscale into a binary image, i.e., one that is simply black and white. Most frequently, we use thresholding as a way to select areas of interest of an image, while ignoring the parts we are not concerned with. We have already done some simple thresholding, in the “Manipulating pixels” section of the Working with scikit-image episode. In that case, we used a simple NumPy array manipulation to separate the pixels belonging to the root system of a plant from the black background. In this episode, we will learn how to use scikit-image functions to perform thresholding. Then, we will use the masks returned by these functions to select the parts of an image we are interested in.
First, import the packages needed for this episode
Simple thresholding
Consider the image data/shapes-01.jpg with a series of
crudely cut shapes set against a white background.
PYTHON
# load the image
shapes01 = iio.imread(uri="data/shapes-01.jpg")
fig, ax = plt.subplots()
ax.imshow(shapes01)
Now suppose we want to select only the shapes from the image. In
other words, we want to leave the pixels belonging to the shapes “on,”
while turning the rest of the pixels “off,” by setting their colour
channel values to zeros. The scikit-image library has several different
methods of thresholding. We will start with the simplest version, which
involves an important step of human input. Specifically, in this simple,
fixed-level thresholding, we have to provide a threshold value
t.
The process works like this. First, we will load the original image, convert it to grayscale, and de-noise it as in the Blurring Images episode.
PYTHON
# convert the image to grayscale
gray_shapes = ski.color.rgb2gray(shapes01)
# blur the image to denoise
blurred_shapes = ski.filters.gaussian(gray_shapes, sigma=1.0)
fig, ax = plt.subplots()
ax.imshow(blurred_shapes, cmap="gray")
Next, we would like to apply the threshold t such that
pixels with grayscale values on one side of t will be
turned “on”, while pixels with grayscale values on the other side will
be turned “off”. How might we do that? Remember that grayscale images
contain pixel values in the range from 0 to 1, so we are looking for a
threshold t in the closed range [0.0, 1.0]. We see in the
image that the geometric shapes are “darker” than the white background
but there is also some light gray noise on the background. One way to
determine a “good” value for t is to look at the grayscale
histogram of the image and try to identify what grayscale ranges
correspond to the shapes in the image or the background.
The histogram for the shapes image shown above can be produced as in the Creating Histograms episode.
PYTHON
# create a histogram of the blurred grayscale image
histogram, bin_edges = np.histogram(blurred_shapes, bins=256, range=(0.0, 1.0))
fig, ax = plt.subplots()
ax.plot(bin_edges[0:-1], histogram)
ax.set_title("Grayscale Histogram")
ax.set_xlabel("grayscale value")
ax.set_ylabel("pixels")
ax.set_xlim(0, 1.0)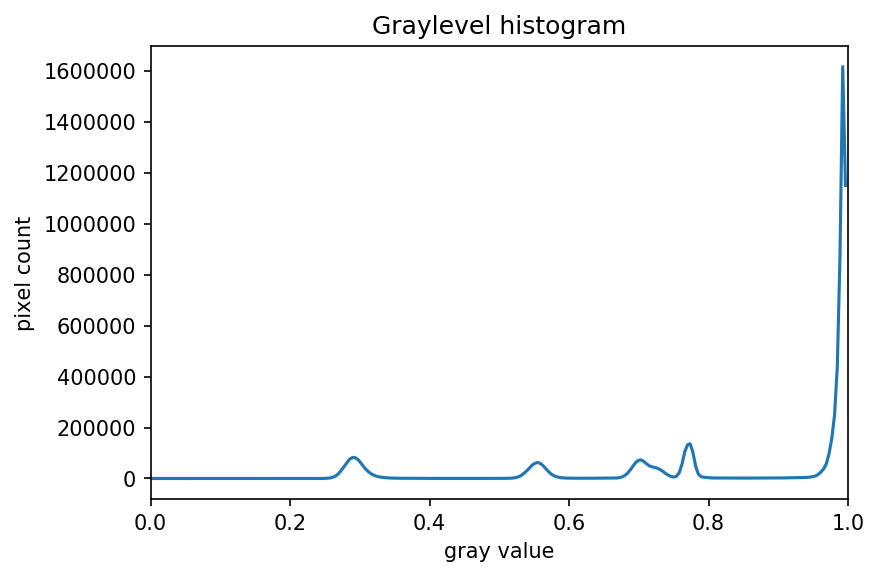
Since the image has a white background, most of the pixels in the
image are white. This corresponds nicely to what we see in the
histogram: there is a peak near the value of 1.0. If we want to select
the shapes and not the background, we want to turn off the white
background pixels, while leaving the pixels for the shapes turned on.
So, we should choose a value of t somewhere before the
large peak and turn pixels above that value “off”. Let us choose
t=0.8.
To apply the threshold t, we can use the NumPy
comparison operators to create a mask. Here, we want to turn “on” all
pixels which have values smaller than the threshold, so we use the less
operator < to compare the blurred_image to
the threshold t. The operator returns a mask, that we
capture in the variable binary_mask. It has only one
channel, and each of its values is either 0 or 1. The binary mask
created by the thresholding operation can be shown with
ax.imshow, where the False entries are shown
as black pixels (0-valued) and the True entries are shown
as white pixels (1-valued).
PYTHON
# create a mask based on the threshold
t = 0.8
binary_mask = blurred_shapes < t
fig, ax = plt.subplots()
ax.imshow(binary_mask, cmap="gray")
You can see that the areas where the shapes were in the original area are now white, while the rest of the mask image is black.
What makes a good threshold?
As is often the case, the answer to this question is “it depends”. In
the example above, we could have just switched off all the white
background pixels by choosing t=1.0, but this would leave
us with some background noise in the mask image. On the other hand, if
we choose too low a value for the threshold, we could lose some of the
shapes that are too bright. You can experiment with the threshold by
re-running the above code lines with different values for
t. In practice, it is a matter of domain knowledge and
experience to interpret the peaks in the histogram so to determine an
appropriate threshold. The process often involves trial and error, which
is a drawback of the simple thresholding method. Below we will introduce
automatic thresholding, which uses a quantitative, mathematical
definition for a good threshold that allows us to determine the value of
t automatically. It is worth noting that the principle for
simple and automatic thresholding can also be used for images with pixel
ranges other than [0.0, 1.0]. For example, we could perform thresholding
on pixel intensity values in the range [0, 255] as we have already seen
in the Working with
scikit-image episode.
We can now apply the binary_mask to the original
coloured image as we have learned in the
Drawing and Bitwise Operations episode. What we are left
with is only the coloured shapes from the original.
PYTHON
# use the binary_mask to select the "interesting" part of the image
selection = shapes01.copy()
selection[~binary_mask] = 0
fig, ax = plt.subplots()
ax.imshow(selection)
More practice with simple thresholding (15 min)
Now, it is your turn to practice. Suppose we want to use simple
thresholding to select only the coloured shapes (in this particular case
we consider grayish to be a colour, too) from the image
data/shapes-02.jpg:

First, plot the grayscale histogram as in the Creating Histogram episode and
examine the distribution of grayscale values in the image. What do you
think would be a good value for the threshold t?
The histogram for the data/shapes-02.jpg image can be
shown with
PYTHON
shapes = iio.imread(uri="data/shapes-02.jpg")
gray_shapes = ski.color.rgb2gray(shapes)
histogram, bin_edges = np.histogram(gray_shapes, bins=256, range=(0.0, 1.0))
fig, ax = plt.subplots()
ax.plot(bin_edges[0:-1], histogram)
ax.set_title("Graylevel histogram")
ax.set_xlabel("gray value")
ax.set_ylabel("pixel count")
ax.set_xlim(0, 1.0)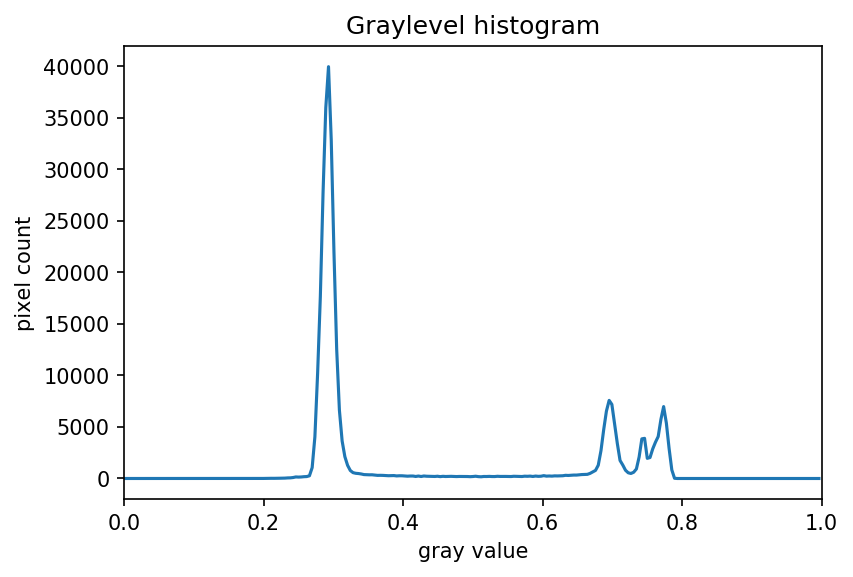
We can see a large spike around 0.3, and a smaller spike around 0.7.
The spike near 0.3 represents the darker background, so it seems like a
value close to t=0.5 would be a good choice.
More practice with simple thresholding (15 min) (continued)
Next, create a mask to turn the pixels above the threshold
t on and pixels below the threshold t off.
Note that unlike the image with a white background we used above, here
the peak for the background colour is at a lower gray level than the
shapes. Therefore, change the comparison operator less <
to greater > to create the appropriate mask. Then apply
the mask to the image and view the thresholded image. If everything
works as it should, your output should show only the coloured shapes on
a black background.
Here are the commands to create and view the binary mask
PYTHON
t = 0.5
binary_mask = gray_shapes > t
fig, ax = plt.subplots()
ax.imshow(binary_mask, cmap="gray")
And here are the commands to apply the mask and view the thresholded image
PYTHON
shapes02 = iio.imread(uri="data/shapes-02.jpg")
selection = shapes02.copy()
selection[~binary_mask] = 0
fig, ax = plt.subplots()
ax.imshow(selection)
Automatic thresholding
The downside of the simple thresholding technique is that we have to
make an educated guess about the threshold t by inspecting
the histogram. There are also automatic thresholding methods
that can determine the threshold automatically for us. One such method
is Otsu’s
method. It is particularly useful for situations where the
grayscale histogram of an image has two peaks that correspond to
background and objects of interest.
Denoising an image before thresholding
In practice, it is often necessary to denoise the image before thresholding, which can be done with one of the methods from the Blurring Images episode.
Consider the image data/maize-root-cluster.jpg of a
maize root system which we have seen before in the Working with scikit-image
episode.
PYTHON
maize_roots = iio.imread(uri="data/maize-root-cluster.jpg")
fig, ax = plt.subplots()
ax.imshow(maize_roots)
We use Gaussian blur with a sigma of 1.0 to denoise the root image. Let us look at the grayscale histogram of the denoised image.
PYTHON
# convert the image to grayscale
gray_image = ski.color.rgb2gray(maize_roots)
# blur the image to denoise
blurred_image = ski.filters.gaussian(gray_image, sigma=1.0)
# show the histogram of the blurred image
histogram, bin_edges = np.histogram(blurred_image, bins=256, range=(0.0, 1.0))
fig, ax = plt.subplots()
ax.plot(bin_edges[0:-1], histogram)
ax.set_title("Graylevel histogram")
ax.set_xlabel("gray value")
ax.set_ylabel("pixel count")
ax.set_xlim(0, 1.0)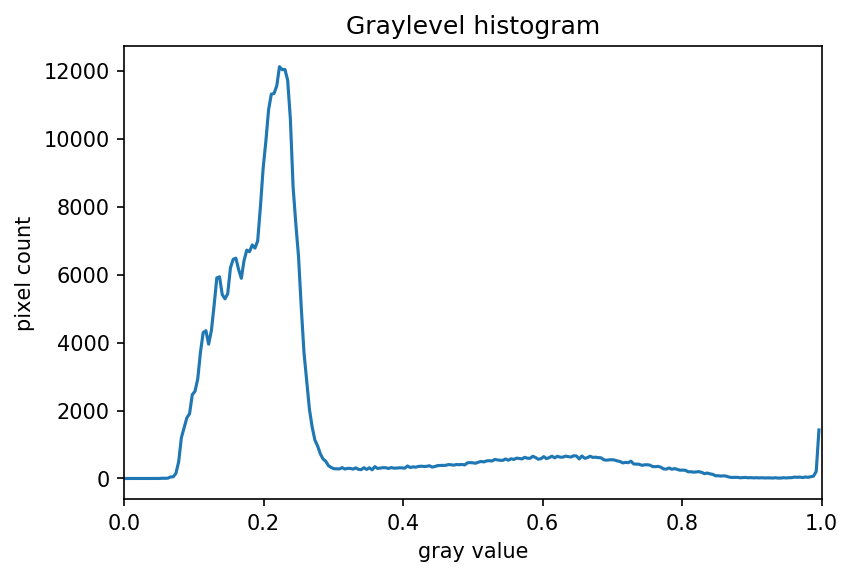
The histogram has a significant peak around 0.2 and then a broader “hill” around 0.6 followed by a smaller peak near 1.0. Looking at the grayscale image, we can identify the peak at 0.2 with the background and the broader peak with the foreground. Thus, this image is a good candidate for thresholding with Otsu’s method. The mathematical details of how this works are complicated (see the scikit-image documentation if you are interested), but the outcome is that Otsu’s method finds a threshold value between the two peaks of a grayscale histogram which might correspond well to the foreground and background depending on the data and application.
The histogram of the maize root image may prompt questions from learners about the interpretation of the peaks and the broader region around 0.6. The focus here is on the separation of background and foreground pixel values. We note that Otsu’s method does not work well for the image with the shapes used earlier in this episode, as the foreground pixel values are more distributed. These examples could be augmented with a discussion of unimodal, bimodal, and multimodal histograms. While these points can lead to fruitful considerations, the text in this episode attempts to reduce cognitive load and deliberately simplifies the discussion.
The ski.filters.threshold_otsu() function can be used to
determine the threshold automatically via Otsu’s method. Then NumPy
comparison operators can be used to apply it as before. Here are the
Python commands to determine the threshold t with Otsu’s
method.
PYTHON
# perform automatic thresholding
t = ski.filters.threshold_otsu(blurred_image)
print("Found automatic threshold t = {}.".format(t))OUTPUT
Found automatic threshold t = 0.4172454549881862.For this root image and a Gaussian blur with the chosen sigma of 1.0,
the computed threshold value is 0.42. No we can create a binary mask
with the comparison operator >. As we have seen before,
pixels above the threshold value will be turned on, those below the
threshold will be turned off.
PYTHON
# create a binary mask with the threshold found by Otsu's method
binary_mask = blurred_image > t
fig, ax = plt.subplots()
ax.imshow(binary_mask, cmap="gray")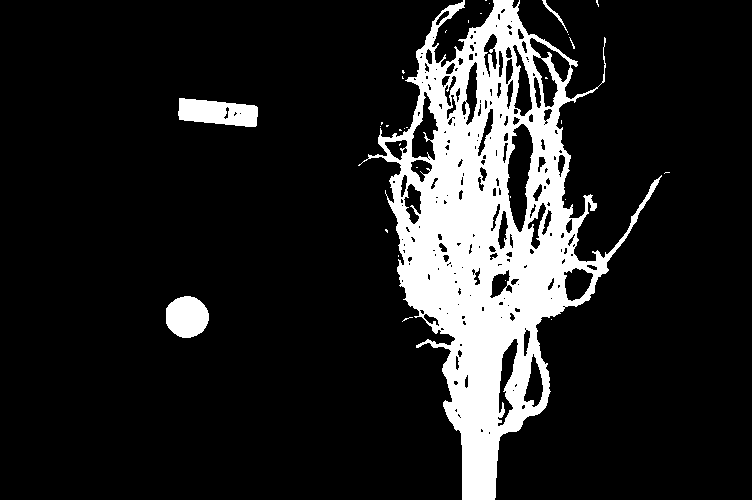
Finally, we use the mask to select the foreground:
PYTHON
# apply the binary mask to select the foreground
selection = maize_roots.copy()
selection[~binary_mask] = 0
fig, ax = plt.subplots()
ax.imshow(selection)
Application: measuring root mass
Let us now turn to an application where we can apply thresholding and
other techniques we have learned to this point. Consider these four
maize root system images, which you can find in the files
data/trial-016.jpg, data/trial-020.jpg,
data/trial-216.jpg, and
data/trial-293.jpg.

Suppose we are interested in the amount of plant material in each image, and in particular how that amount changes from image to image. Perhaps the images represent the growth of the plant over time, or perhaps the images show four different maize varieties at the same phase of their growth. The question we would like to answer is, “how much root mass is in each image?”
We will first construct a Python program to measure this value for a single image. Our strategy will be this:
- Read the image, converting it to grayscale as it is read. For this application we do not need the colour image.
- Blur the image.
- Use Otsu’s method of thresholding to create a binary image, where the pixels that were part of the maize plant are white, and everything else is black.
- Save the binary image so it can be examined later.
- Count the white pixels in the binary image, and divide by the number of pixels in the image. This ratio will be a measure of the root mass of the plant in the image.
- Output the name of the image processed and the root mass ratio.
Our intent is to perform these steps and produce the numeric result - a measure of the root mass in the image - without human intervention. Implementing the steps within a Python function will enable us to call this function for different images.
Here is a Python function that implements this root-mass-measuring strategy. Since the function is intended to produce numeric output without human interaction, it does not display any of the images. Almost all of the commands should be familiar, and in fact, it may seem simpler than the code we have worked on thus far, because we are not displaying any of the images.
PYTHON
def measure_root_mass(filename, sigma=1.0):
# read the original image, converting to grayscale on the fly
image = iio.imread(uri=filename, mode="L")
# blur before thresholding
blurred_image = ski.filters.gaussian(image, sigma=sigma)
# perform automatic thresholding to produce a binary image
t = ski.filters.threshold_otsu(blurred_image)
binary_mask = blurred_image > t
# determine root mass ratio
root_pixels = np.count_nonzero(binary_mask)
density = root_pixels / binary_mask.size
return densityThe function begins with reading the original image from the file
filename. We use iio.imread() with the
optional argument mode="L" to automatically convert it to
grayscale. Next, the grayscale image is blurred with a Gaussian filter
with the value of sigma that is passed to the function.
Then we determine the threshold t with Otsu’s method and
create a binary mask just as we did in the previous section. Up to this
point, everything should be familiar.
The final part of the function determines the root mass ratio in the
image. Recall that in the binary_mask, every pixel has
either a value of zero (black/background) or one (white/foreground). We
want to count the number of white pixels, which can be accomplished with
a call to the NumPy function np.count_nonzero. Finally, the
density ratio is calculated by dividing the number of white pixels by
the total number of pixels binary_mask.size in the image.
The function returns then root density of the image.
We can call this function with any filename and provide a sigma value
for the blurring. If no sigma value is provided, the default value 1.0
will be used. For example, for the file data/trial-016.jpg
and a sigma value of 1.5, we would call the function like this:
OUTPUT
0.0482436835106383`Now we can use the function to process the series of four images shown above. In a real-world scientific situation, there might be dozens, hundreds, or even thousands of images to process. To save us the tedium of calling the function for each image by hand, we can write a loop that processes all files automatically. The following code block assumes that the files are located in the same directory and the filenames all start with the trial- prefix and end with the .jpg suffix.
PYTHON
all_files = glob.glob("data/trial-*.jpg")
for filename in all_files:
density = measure_root_mass(filename=filename, sigma=1.5)
# output in format suitable for .csv
print(filename, density, sep=",")OUTPUT
data/trial-016.jpg,0.0482436835106383
data/trial-020.jpg,0.06346941489361702
data/trial-216.jpg,0.14073969414893617
data/trial-293.jpg,0.13607895611702128Ignoring more of the images – brainstorming (10 min)
Let us take a closer look at the binary masks produced by the
measure_root_mass function.
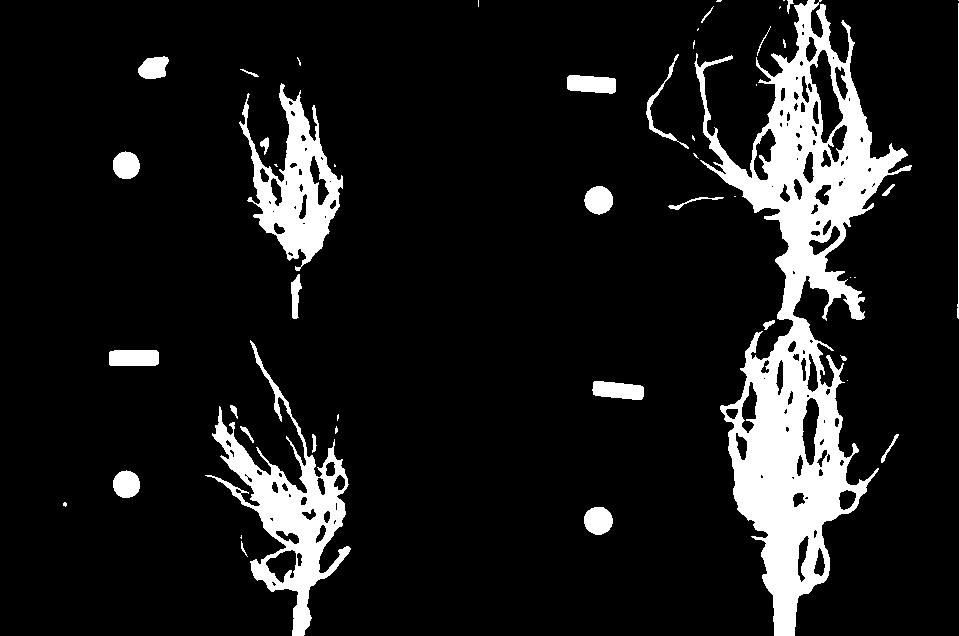
You may have noticed in the section on automatic thresholding that the thresholded image does include regions of the image aside of the plant root: the numbered labels and the white circles in each image are preserved during the thresholding, because their grayscale values are above the threshold. Therefore, our calculated root mass ratios include the white pixels of the label and white circle that are not part of the plant root. Those extra pixels affect how accurate the root mass calculation is!
How might we remove the labels and circles before calculating the ratio, so that our results are more accurate? Think about some options given what we have learned so far.
One approach we might take is to try to completely mask out a region from each image, particularly, the area containing the white circle and the numbered label. If we had coordinates for a rectangular area on the image that contained the circle and the label, we could mask the area out by using techniques we learned in the Drawing and Bitwise Operations episode.
However, a closer inspection of the binary images raises some issues with that approach. Since the roots are not always constrained to a certain area in the image, and since the circles and labels are in different locations each time, we would have difficulties coming up with a single rectangle that would work for every image. We could create a different masking rectangle for each image, but that is not a practicable approach if we have hundreds or thousands of images to process.
Another approach we could take is to apply two thresholding steps to
the image. Look at the graylevel histogram of the file
data/trial-016.jpg shown above again: Notice the peak near
1.0? Recall that a grayscale value of 1.0 corresponds to white pixels:
the peak corresponds to the white label and circle. So, we could use
simple binary thresholding to mask the white circle and label from the
image, and then we could use Otsu’s method to select the pixels in the
plant portion of the image.
Note that most of this extra work in processing the image could have been avoided during the experimental design stage, with some careful consideration of how the resulting images would be used. For example, all of the following measures could have made the images easier to process, by helping us predict and/or detect where the label is in the image and subsequently mask it from further processing:
- Using labels with a consistent size and shape
- Placing all the labels in the same position, relative to the sample
- Using a non-white label, with non-black writing
Ignoring more of the images – implementation (30 min - optional, not included in timing)
Implement an enhanced version of the function
measure_root_mass that applies simple binary thresholding
to remove the white circle and label from the image before applying
Otsu’s method.
We can apply a simple binary thresholding with a threshold
t=0.95 to remove the label and circle from the image. We
can then use the binary mask to calculate the Otsu threshold without the
pixels from the label and circle.
PYTHON
def enhanced_root_mass(filename, sigma):
# read the original image, converting to grayscale on the fly
image = iio.imread(uri=filename, mode="L")
# blur before thresholding
blurred_image = ski.filters.gaussian(image, sigma=sigma)
# perform binary thresholding to mask the white label and circle
binary_mask = blurred_image < 0.95
# perform automatic thresholding using only the pixels with value True in the binary mask
t = ski.filters.threshold_otsu(blurred_image[binary_mask])
# update binary mask to identify pixels which are both less than 0.95 and greater than t
binary_mask = (blurred_image < 0.95) & (blurred_image > t)
# determine root mass ratio
root_pixels = np.count_nonzero(binary_mask)
density = root_pixels / binary_mask.size
return density
all_files = glob.glob("data/trial-*.jpg")
for filename in all_files:
density = enhanced_root_mass(filename=filename, sigma=1.5)
# output in format suitable for .csv
print(filename, density, sep=",")The output of the improved program does illustrate that the white circles and labels were skewing our root mass ratios:
OUTPUT
data/trial-016.jpg,0.046250166223404256
data/trial-020.jpg,0.05886968085106383
data/trial-216.jpg,0.13712117686170214
data/trial-293.jpg,0.13190342420212767The & operator above means that we have defined a
logical AND statement. This combines the two tests of pixel intensities
in the blurred image such that both must be true for a pixel’s position
to be set to True in the resulting mask.
Result of t < blurred_image
|
Result of blurred_image < 0.95
|
Resulting value in binary_mask
|
|---|---|---|
| False | True | False |
| True | False | False |
| True | True | True |
Knowing how to construct this kind of logical operation can be very helpful in image processing. The University of Minnesota Library’s guide to Boolean operators is a good place to start if you want to learn more.
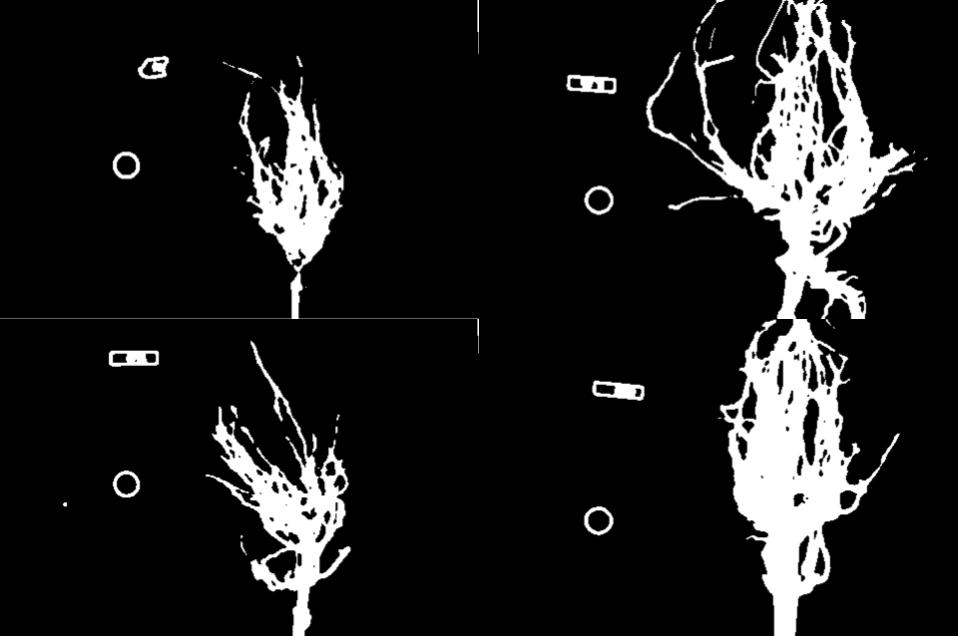
Here are the binary images produced by the additional thresholding. Note that we have not completely removed the offending white pixels. Outlines still remain. However, we have reduced the number of extraneous pixels, which should make the output more accurate.
Thresholding a bacteria colony image (15 min)
In the images directory data/, you will find an image
named colonies-01.tif.
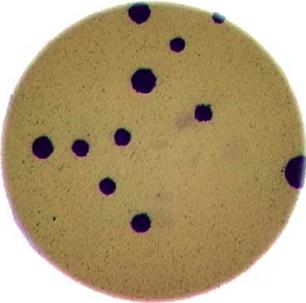
This is one of the images you will be working with in the morphometric challenge at the end of the workshop.
- Plot and inspect the grayscale histogram of the image to determine a good threshold value for the image.
- Create a binary mask that leaves the pixels in the bacteria colonies “on” while turning the rest of the pixels in the image “off”.
Here is the code to create the grayscale histogram:
PYTHON
bacteria = iio.imread(uri="data/colonies-01.tif")
gray_image = ski.color.rgb2gray(bacteria)
blurred_image = ski.filters.gaussian(gray_image, sigma=1.0)
histogram, bin_edges = np.histogram(blurred_image, bins=256, range=(0.0, 1.0))
fig, ax = plt.subplots()
ax.plot(bin_edges[0:-1], histogram)
ax.set_title("Graylevel histogram")
ax.set_xlabel("gray value")
ax.set_ylabel("pixel count")
ax.set_xlim(0, 1.0)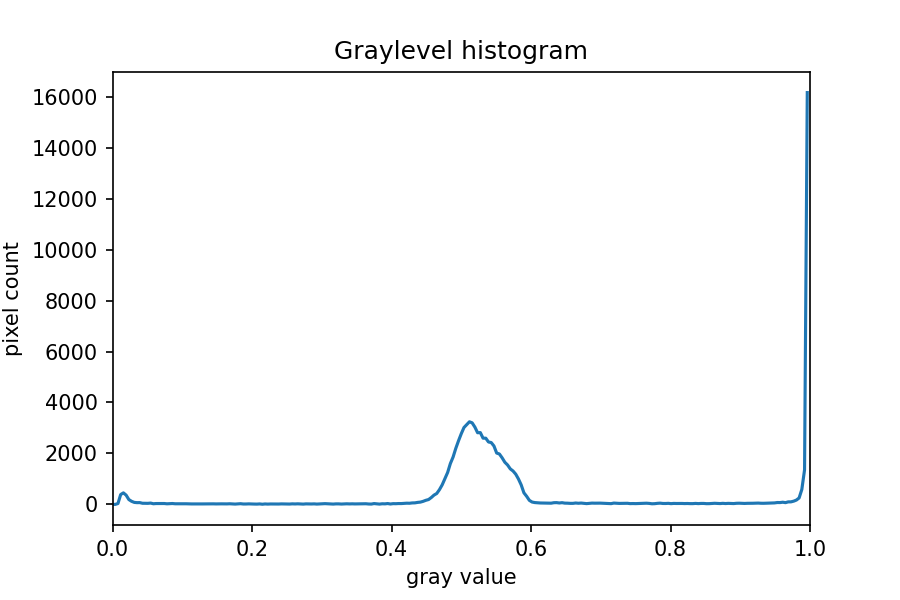
The peak near one corresponds to the white image background, and the
broader peak around 0.5 corresponds to the yellow/brown culture medium
in the dish. The small peak near zero is what we are after: the dark
bacteria colonies. A reasonable choice thus might be to leave pixels
below t=0.2 on.
Here is the code to create and show the binarized image using the
< operator with a threshold t=0.2:
PYTHON
t = 0.2
binary_mask = blurred_image < t
fig, ax = plt.subplots()
ax.imshow(binary_mask, cmap="gray")
When you experiment with the threshold a bit, you can see that in particular the size of the bacteria colony near the edge of the dish in the top right is affected by the choice of the threshold.
- Thresholding produces a binary image, where all pixels with intensities above (or below) a threshold value are turned on, while all other pixels are turned off.
- The binary images produced by thresholding are held in two-dimensional NumPy arrays, since they have only one colour value channel. They are boolean, hence they contain the values 0 (off) and 1 (on).
- Thresholding can be used to create masks that select only the interesting parts of an image, or as the first step before edge detection or finding contours.
