Making the Isochrone DataFrame
Last updated on 2023-05-15 | Edit this page
Calculating Isochrone
In fact, we can use MESA Isochrones & Stellar Tracks (MIST) to compute it for us. Using the MIST Version 1.2 web interface, we computed an isochrone with the following parameters:
- Rotation initial v/v_crit = 0.4
- Single age, linear scale = 12e9
- Composition [Fe/H] = -1.35
- Synthetic Photometry, PanStarrs
- Extinction av = 0
The following cell downloads the results:
PYTHON
download('https://github.com/AllenDowney/AstronomicalData/raw/main/' +
'data/MIST_iso_5fd2532653c27.iso.cmd')To read this file we will download a Python module from this repository.
PYTHON
download('https://github.com/jieunchoi/MIST_codes/raw/master/scripts/' +
'read_mist_models.py')Now we can read the file:
PYTHON
import read_mist_models
filename = 'MIST_iso_5fd2532653c27.iso.cmd'
iso = read_mist_models.ISOCMD(filename)OUTPUT
Reading in: MIST_iso_5fd2532653c27.iso.cmdThe result is an ISOCMD object.
OUTPUT
read_mist_models.ISOCMDIt contains a list of arrays, one for each isochrone.
OUTPUT
listWe only got one isochrone.
OUTPUT
1So we can select it like this:
It is a NumPy array:
OUTPUT
numpy.ndarrayBut it is an unusual NumPy array, because it contains names for the columns.
OUTPUT
dtype([('EEP', '<i4'), ('isochrone_age_yr', '<f8'), ('initial_mass', '<f8'), ('star_mass', '<f8'), ('log_Teff', '<f8'), ('log_g', '<f8'), ('log_L', '<f8'), ('[Fe/H]_init', '<f8'), ('[Fe/H]', '<f8'), ('PS_g', '<f8'), ('PS_r', '<f8'), ('PS_i', '<f8'), ('PS_z', '<f8'), ('PS_y', '<f8'), ('PS_w', '<f8'), ('PS_open', '<f8'), ('phase', '<f8')])Which means we can select columns using the bracket operator:
OUTPUT
array([0., 0., 0., ..., 6., 6., 6.])We can use phase to select the part of the isochrone for
stars in the main sequence and red giant phases.
OUTPUT
354OUTPUT
354The other two columns we will use are PS_g and
PS_i, which contain simulated photometry data for stars
with the given age and metallicity, based on a model of the Pan-STARRS
sensors.
We will use these columns to superimpose the isochrone on the color-magnitude diagram, but first we have to use a distance modulus to scale the isochrone based on the estimated distance of GD-1.
We can use the Distance object from Astropy to compute
the distance modulus.
PYTHON
import astropy.coordinates as coord
import astropy.units as u
distance = 7.8 * u.kpc
distmod = coord.Distance(distance).distmod.value
distmodOUTPUT
14.4604730134524Now we can compute the scaled magnitude and color of the isochrone.
PYTHON
mag_g = main_sequence['PS_g'] + distmod
color_g_i = main_sequence['PS_g'] - main_sequence['PS_i']Now we can plot it on the color-magnitude diagram like this.
OUTPUT
<Figure size 432x288 with 1 Axes>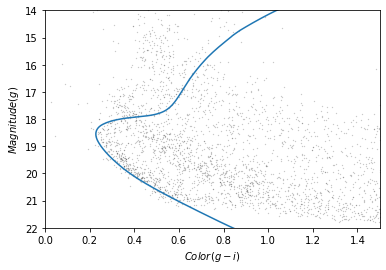
The theoretical isochrone passes through the overdense region where we expect to find stars in GD-1.
We will save this result so we can reload it later without repeating the steps in this section.
So we can save the data in an HDF5 file, we will put it in a Pandas
DataFrame first:
PYTHON
import pandas as pd
iso_df = pd.DataFrame()
iso_df['mag_g'] = mag_g
iso_df['color_g_i'] = color_g_i
iso_df.head()OUTPUT
mag_g color_g_i
0 28.294743 2.195021
1 28.189718 2.166076
2 28.051761 2.129312
3 27.916194 2.093721
4 27.780024 2.058585And then save it.
